Une nouvelle approche du transport de sédiment pour les rivières de montagne
L’article passe en revue nos récentes tentatives de modélisation du transport solide dans les rivières de montagne. C’est un problème de longue date qui a attiré beaucoup d’attention au cours du dernier siècle. Si un certain nombre d’études de terrain et de laboratoire ont permis d’obtenir une vue d’ensemble, il manque toujours des méthodes efficaces pour prédire l’évolution du lit et le transport solide. La plupart des approches du transport solide ont supposé l’existence d’une relation univoque entre débits solide et liquide, mais cette hypothèse est contredite par la dispersion des données, qui s’étendent souvent sur plusieurs ordres de grandeur : en effet, à un débit liquide donné est associé une large gamme de débits solides possibles.
Dans notre approche, l’hypothèse de travail est que les fluctuations du transport solide gouvernent la dynamique d’ensemble du transport. Nous avons développé un modèle théorique basé sur les processus de Markov dit de « mort-naissance », qui décrit les échanges aléatoires entre l’écoulement d’eau et le lit. On aboutit à une équation pour les fluctuations du nombre de particules en mouvement. Nous pouvons alors calculer la fonction de distribution de probabilité du débit solide. Une caractéristique remarquable prédite par ce modèle est l’existence de grandes fluctuations même en régime permanent.
1. Introduction
L’objectif de cet article est de présenter une approche innovante des sédiments transport. Le projet en cours vise à fournir une quantification plus précise du transport de sédiment dans les rivières à lit de gravier, avec une attention particulière portée aux torrents de montagne. Malgré des décennies de recherche, le transport de sédiments reste un problème difficile, en particulier pour les rivières avec des lits en gravier. Par exemple, la figure1 montre le débit solide mesuré dans une rivière torrentielle, la Navisence à Zinal de 2011 à 2013 (le débit est moyenné sur 1 min) en fonction du transport prédit par une formule empire, l’équation de Meunier, qui lie le débit solide Qs (en kg/s) au débit liquide Q w (en m3/s) et de la pente du lit i comme suit [1] :
On pourrait employer des équations plus complètes, mais elles conduiraient à des erreurs similaires voire plus importantes. À faible débit, l’écart entre l’équation empirique et les mesures dépasse trois ordres de grandeur. Même aux débits les plus forts (pour la crue du 8 août 2013, la période de retour était proche de 50 ans), l’écart entre formule et données est considérable. Cet exemple montre à quel point notre capacité prédictive du transport solide est médiocre lorsque des équations empiriques sont utilisées.
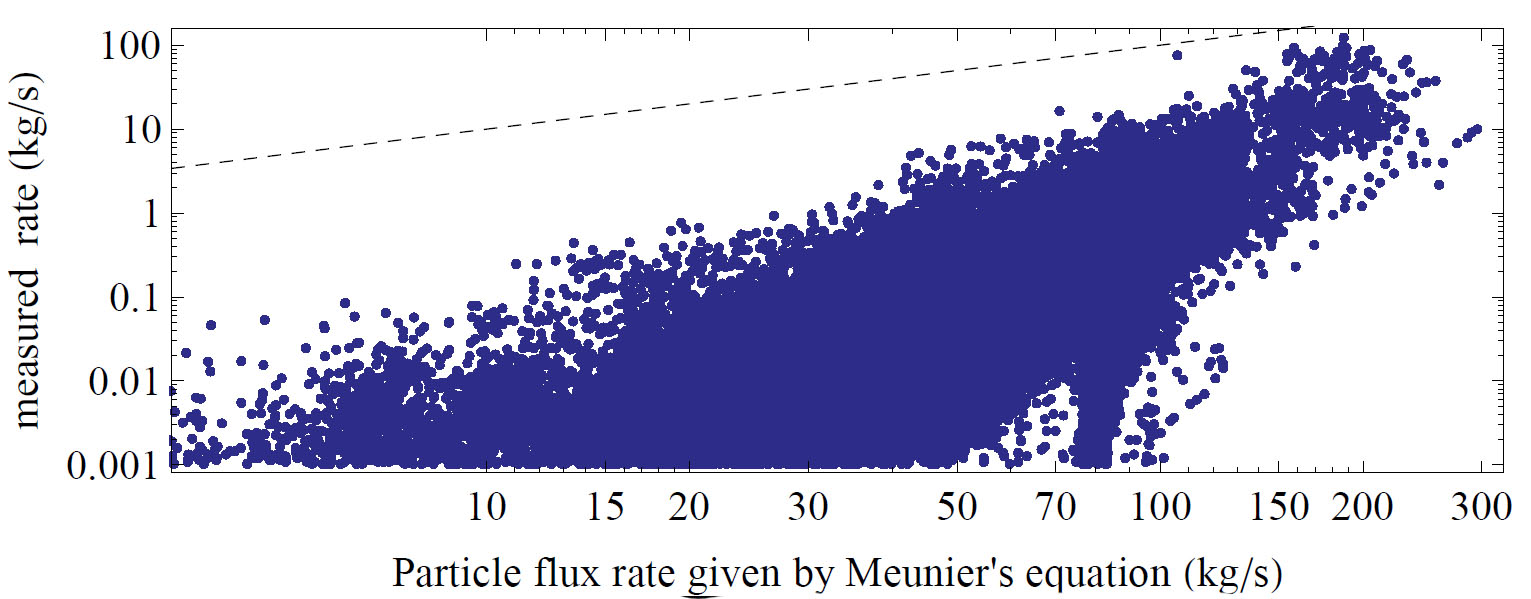
Figure 1 : Comparaison entre les mesures de débit solide et l’équation de Meunier pour la rivière Navisence (Zinal, VS). Ici la pente locale en amont de la station est i = 3,2%.
Cette lacune est connue depuis longtemps, bien que la plupart des ouvrages sur le sujet mentionnent à peine l’énorme incertitude associée à la prédiction débit solide (sans parler de l’utilisation systématique de diagrammes log-log qui minimise la perception des erreurs et des écarts). Chaque génération de scientifiques a abordé cette question en arguant que plus de physique est nécessaire pour aborder correctement le problème en question. Dans les années 1950, Hans Einstein a proposé un modèle de transport solide selon lequel le transport résulte de la différence entre l’entraînement et la déposition, E et D, respectivement, qui dépendent des conditions d’écoulement et la géométrie du lit [2]. Cela revient à écrire que sur un petit intervalle Δ x, la variation de flux de particules est
et de sorte que le flux de particules à l’ équilibre est la solution implicite de l’équation E = D. L’originalité du traitement d’Einstein réside dans l’introduction de concepts probabilistes pour quantifier la probabilité d’entraînement d’une particule reposant sur le lit. Dans les années 1960, Ralph Bagnold a considéré le transport des sédiments comme régi par des transferts de quantité de mouvement entre les phases solide et liquide [3]. Pour lui, le transport solide est essentiellement un écoulement à deux phases dont la dynamique est contrôlée par transferts de quantité de mouvement entre l’eau et la phase solide. Inutile de dire qu’après des décennies d’études, le débat est toujours ouvert. Pour mieux comprendre le transport des sédiments, nous devons identifier les difficultés spécifiques à construction des théories sur le transport sédimentaire (rappelons que l’accent est mis sur le charriage torrentiel, le transport de sédiment fin par suspension est sans doute plus simple).